Question

Conversion of mass to moles A continuous feed to a separation unit is 1,000 kg/h of 45 wt% methanol and 55 wt% water, whose molecular weights are 32 and 18, respectively. Compute: (a) feed rate in lbmol/h, and (b) composition in mole fractions.

Answer 1

Total feed rate = 98.3 lbmol/h

methanol mole fraction = 0.315

water mole fraction = 0.685

Step-by-step explanation:

First of all, it is needed to calculate the feed mass of methanol and water in kg/h.

For methanol:

`m_(methanol) = m\%wt_(methanol)/100 = (1000kg/h)(45\%)/100`

`m_(methanol) = 450kg/h`

For water:

`m_(water) = m\%wt_(water)/100 = (1000kg/h)(55\%)/100`

`m_(water) = 550 kg/h`

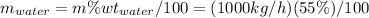
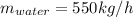
Now, change from mass units (kg/h) to moles units (kmol/h and lbmol/h) using simple conversion factors:

For methanol:

`n_(methanol) = (450(kg)/(h))((1 kmol)/(32 kg) )`

`n_(methanol) = 14.1kmol/h`

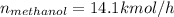
For water:

`n_(water) = (550(kg)/(h))((1 kmol)/(18 kg) )`

`n_(water) = 30.6kmol/h`

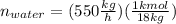
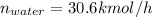
Change units from kmol/h to lbmol/h

For methanol:

`n_(methanol) = (14.1(kmol)/(h))((1 lbmol)/(0.454 kmol) )`

`n_(methanol) = 31.0 lbmol/h`

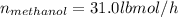
For water:

`n_(water) = (30.6(kg)/(h))((1 lbmol)/(0.454 kmol) )`

`n_(water) = 67.3 lbmol/h`

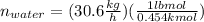
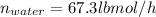
Sum moles of methanol and water in lbmol/h to compute the total feed rate:

`n = 31.0 lbmol/h + 67.3 lbmol/h`

`n = 98.3 lbmol/h`

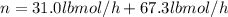
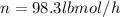
Divide both methanol and water moles feed rates by total feed rate:

For methanol:

`X_(methanol) = (31.0 lbmol/h)/(98.3 lbmol/h)`

`X_(methanol) =  0.315`

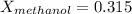
For water:

`[X_(water) =  (67.3 lbmol/h)/(98.3 lbmol/h)`

`X_(water) =  0.685`

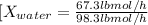
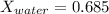
End