Question

Water (10 kg/s) at 1 bar pressure and 50 C is pumped isothermally to 10 bar. What is the pump work? (Use the steam tables.) O -7.3J/s O 7.3 kJ/s O -210 kJ/s O 3451 kJ/s

Answer 1

Step-by-step explanation:

For an isothermal process equation will be as follows.

W = nRT ln
`(P_(1))/(P_(2))`

It is given that mass is 10 kg/s or 10,000 g/s (as 1 kg = 1000 g). So, calculate number of moles of water as follows.

No. of moles =
`\frac{mass}{\text{molar mass}}`

=
`(10000 g/s)/(18 g/mol)`

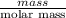
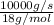
= 555.55 mol/s

= 556 mol/s (approx)

As T =
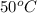`50^(o)C` or (50 + 273.15) K = 323.15 K. Hence, putting the given values into the above formula as follows.

W = nRT ln[/tex]\frac{P_{1}}{P_{2}}[/tex]

=
`556 mol/s * 8.314 J/ K mol K * 323.15 K * ln(1)/(10)`

=
`556 mol/s * 8.314 J/ K mol K * 323.15 K * -2.303`

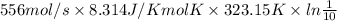
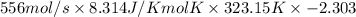
= -3440193.809 J/s

Negative sign shows work is done by the pump. Since, 1 J = 0.001 kJ. Therefore, converting the calculated value into kJ as follows.

`3440193.809 J/s * (0.001 kJ)/(1 J)`

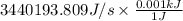
= 3440.193 kJ/s

= 3451 kJ/s (approx)

Thus, we can conclude that the pump work is 3451 kJ/s.