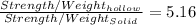Answer with Explanation:
By the equation or Torque we have
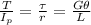
where
T is the torque applied on the shaft
 is the polar moment of inertia of the shaft
is the polar moment of inertia of the shaft
 is the shear stress developed at a distance 'r' from the center of the shaft
is the shear stress developed at a distance 'r' from the center of the shaft
 is the angle of twist of the shaft
is the angle of twist of the shaft
'G' is the modulus of rigidity of the shaft
We know that for solid shaft
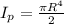
For a hollow shaft
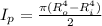
Since the two shafts are subjected to same torque from the relation of Torque we have
1) For solid shaft
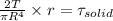
2) For hollow shaft we have
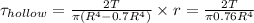
Comparing the above 2 relations we see
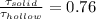
Similarly for angle of twist we can see
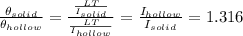
Part b)
Strength of solid shaft =

Weight of solid shaft =
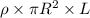
Strength per unit weight of solid shaft =

Strength of hollow shaft =
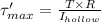
Weight of hollow shaft =
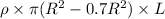
Strength per unit weight of hollow shaft =
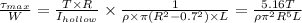
Thus