Question

The halpy of vaporization of H2O at 1 atm and 100 C is 2259 kJ/kg. The heat capacity of liquid water is 4.19 kJ/kg.C, and the heat capacity of water vapor is 1.9 kJ/kg-C. H20 at 10 bar boils at 179.9 C. What is the enthalpy of vaporization of H20 at 10 bar? You can neglect the effect of pressure. e 2076 kJ/kg e 1924 kJ/kg e 2259 kJ/kg 2442 kJ/kg 2594 kJ/kg None of the above

Answer 1

Answer: Option (a) is the correct answer.

Step-by-step explanation:

The given data is as follows.

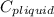`C_(p)_(liquid)` = 4.19
`kJ/kg ^(o)C`

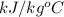
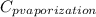`C_(p)_(vaporization)` = 1.9
`kJ/kg ^(o)C`

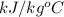
Heat of vaporization (
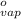`\DeltaH^(o)_(vap)`) at 1 atm and
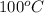`100^(o)C` is 2259 kJ/kg

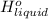`H^(o)_(liquid)` = 0

Therefore, calculate the enthalpy of water vapor at 1 atm and
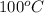`100^(o)C` as follows.

`H^(o)_(vap)` =
`H^(o)_(liquid)` +
`\DeltaH^(o)_(vap)`

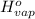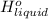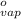
= 0 + 2259 kJ/kg

= 2259 kJ/kg

As the desired temperature is given
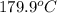`179.9^(o)C` and effect of pressure is not considered. Hence, enthalpy of liquid water at 10 bar and
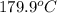`179.9^(o)C` is calculated as follows.

`H^(D)_(liq) = H^(o)_(liquid) + C_(p)_(liquid)(T_(D) - T_(o))`

=
`0 + 4.19 kJ/kg ^(o)C * (179.9^(o)C - 100^(o)C)`

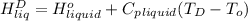
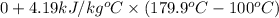
= 334.781 kJ/kg

Hence, enthalpy of water vapor at 10 bar and
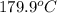`179.9^(o)C` is calculated as follows.

`H^(D)_(vap) = H^(o)_(vap) + C_(p)_(vap) * (T_(D) - T_(o))`

`H^(D)_(vap)` =
`2259 kJ/kg + 1.9 * (179.9 - 100)`

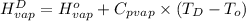
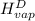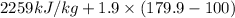
= 2410.81 kJ/kg

Therefore, calculate the latent heat of vaporization at 10 bar and
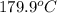`179.9^(o)C` as follows.

`\Delta H^(D)_(vap)` =
`H^(D)_(vap) - H^(D)_(liq)`

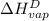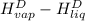
= 2410.81 kJ/kg - 334.781 kJ/kg

= 2076.029 kJ/kg

or, = 2076 kJ/kg

Thus, we can conclude that at 10 bar and
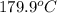`179.9^(o)C` latent heat of vaporization is 2076 kJ/kg.