Question

A body is moving with simple harmonic motion. It's velocity is recorded as being 3.5m/s when it is at 150mm from the mid-position and 2.5m/s when 225mm from mid-position. Find : i) It's max amplitude ii) Max acceleration iii) The periodic time iv) The frequency of oscillation.

Answer 1

1) A=282.6 mm

2)
`a_(max)=60.35\ m/s^2`

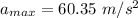
3)T=0.42 sec

4)f= 2.24 Hz

Step-by-step explanation:

Given that

V=3.5 m/s at x=150 mm ------------1

V=2.5 m/s at x=225 mm ------------2

Where x measured from mid position.

We know that velocity in simple harmonic given as

`V=\omega √(A^2-x^2)`

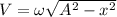
Where A is the amplitude and ω is the natural frequency of simple harmonic motion.

From equation 1 and 2

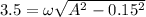`3.5=\omega √(A^2-0.15^2)` ------3

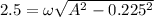`2.5=\omega √(A^2-0.225^2)` --------4

Now by dividing equation 3 by 4

`(3.5)/(2.5)=\frac {√(A^2-0.15^2)}{√(A^2-0.225^2)}`

`1.96=\frac {{A^2-0.15^2}}{{A^2-0.225^2}}`

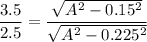
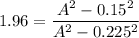
So A=0.2826 m

A=282.6 mm

Now by putting the values of A in the equation 3

`3.5=\omega √(A^2-0.15^2)`

`3.5=\omega √(0.2826^2-0.15^2)`

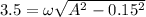
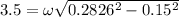
ω=14.609 rad/s

Frequency

ω= 2πf

14.609= 2 x π x f

f= 2.24 Hz

Maximum acceleration

`a_(max)=\omega ^2A`

`a_(max)=14.61 ^2* 0.2826\ m/s^2`

`a_(max)=60.35\ m/s^2`

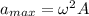
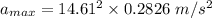
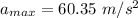
Time period T

`T=(2\pi)/(\omega)`

`T=(2\pi)/(14.609)`

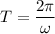
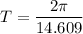
T=0.42 sec