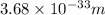Question

Calculate the de Broglie wavelength of a shotgun

pelletweighing 1.2 g moving at a velocity of 150 m/s.

Answer 1

Answer : The de Broglie wavelength will be
`3.68* 10^(-33)m`

Solution :

The formula used for de Broglie wavelength is:

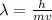`\lambda=(h)/(mv)` ..........(1)

where,

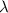`\lambda` = wavelength = ?

h = Planck's constant =
`6.626* 10^(-34)Js`

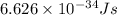
m = mass = 1.2 g = 0.0012 kg

Conversion used : 1 kg = 1000 g

v = velocity = 150 m/s

Now put all the given values in equation 1, we get:

`\lambda=(6.626* 10^(-34)Js)/((0.0012kg)* (150m/s))`

`\lambda=3.68* 10^(-33)m`

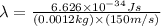
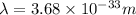
Therefore, the de Broglie wavelength will be
`3.68* 10^(-33)m`