Question

Use Newton's law of universal gravitation to calculate the weight of a 90 kg person standing on the surface of the earth to the nearest 1 N.

Answer 1

W=884 N

Step-by-step explanation:

Hello, I think I can help you with this

the law of universal gravitation predicts that the force exerted between two bodies of masses and separated by a distance is equal to the product of their masses and inversely proportional to the square of the distance, that is:it is given by

`F=G (m_(1) *m_(2) )/(r^(2)) \\\\`

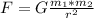
where

G is is the universal gravitation constant.

`G=6.67384 *10^(-11)(Nm^(2) )/(kg^(2)) \\`

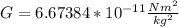
m1 and m2 are the masses of the objects

and r is the distance between the objects

Step 1

to solve this you are going to need the mass of the earth, and the radius of the earth(average)

Radius of the earth=6371 km=6371000 m

mass of the earth=
`5.972 *10^(24)\ Kg\\`

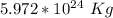
Let

m1=90 kg

m2=
`5.972 *10^(24)\ Kg\\`

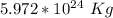
r=6371 km

`G=6.67384 *10^(-11)(Nm^(2) )/(kg^(2))`

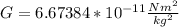
just put the values in the equation

`F=G (m_(1) *m_(2) )/(r^(2))\\F=6.67384 *10^(-11)(Nm^(2) )/(kg^(2) )  (90 kg*5.972 *10^(24)\ Kg)/((6371 000m)^(2) )\\F=(3.58*10^(16) N)/(4.058*10^(13) ) \\F=884 N\\`

Have a good day.