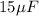Question

Capacitances of 10uF and 20uF are connected in parallel,

andthis pair is then connected in series with a 30-uF capacitor.
What is the equivalent capacitance of this arrangement?

Answer 1

The equivalent capacitance will be
`15\mu F`

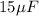
Step-by-step explanation:

We have given two capacitance
`C_=10\mu F\ and\ C_2=20\mu F`

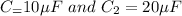
They are connected in parallel

So equivalent capacitance
`C=C_1+C_2=10+20=30\mu F`

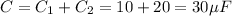
This equivalent capacitance is now connected in series with
`30\mu F`

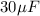
In series combination of capacitors the equivalent capacitance is given by
`(1)/(C)=(1)/(30)+(1)/(30)`

`C=(30)/(2)=15\mu F`

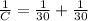
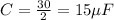
So the equivalent capacitance will be
`15\mu F`