Question

A liquid mixture composed of 20% CH4, 30% C2H4, 35% C2H2, and 15% C2H20. What is the average molecular weight of the mixture? a) 20 b) 25 c) 6.75 d) 9.25

Answer 1

Answer: The correct answer is Option c.

Step-by-step explanation:

We are given:

Mass percentage of
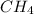`CH_4` = 20 %

So, mole fraction of
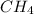`CH_4` = 0.2

Mass percentage of
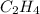`C_2H_4` = 30 %

So, mole fraction of
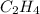`C_2H_4` = 0.3

Mass percentage of
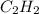`C_2H_2` = 35 %

So, mole fraction of
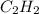`C_2H_2` = 0.35

Mass percentage of
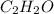`C_2H_2O` = 15 %

So, mole fraction of
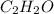`C_2H_2O` = 0.15

We know that:

Molar mass of
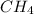`CH_4` = 16 g/mol

Molar mass of
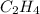`C_2H_4` = 28 g/mol

Molar mass of
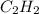`C_2H_2` = 26 g/mol

Molar mass of
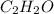`C_2H_2O` = 48 g/mol

To calculate the average molecular mass of the mixture, we use the equation:

`\text{Average molecular weight of mixture}=\frac{_(i=1)^n\sum{\chi_im_i}}{n_i}`

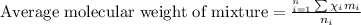
where,

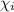`\chi_i` = mole fractions of i-th species

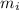`m_i` = molar masses of i-th species

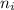`n_i` = number of observations

Putting values in above equation:

`\text{Average molecular weight}=((\chi_(CH_4)* M_(CH_4))+(\chi_(C_2H_4)* M_(C_2H_4))+(\chi_(C_2H_2)* M_(C_2H_2))+(\chi_(C_2H_2O)* M_(C_2H_2O)))/(4)`

`\text{Average molecular weight of mixture}=((0.20* 16)+(0.30* 28)+(0.35* 26)+(0.15* 42))/(4)\\\\\text{Average molecular weight of mixture}=6.75`

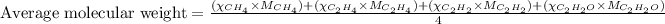
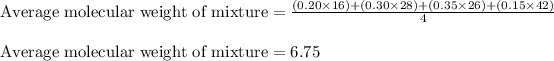
Hence, the correct answer is Option c.