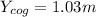Question

A person is standing on a level floor. His head,

uppertorso, arms, and hands together weigh 438 N and have a center
ofgravity that is 1.28 m above the floor. His upper legs weigh 144
Nand have a center of gravity that is 0.760 m above the
floor.Finally, his lower legs and feet together weigh 87 N and
havea center of gravity that is 0.250 m above the floor. Relative
tothe floor, find the location of the center of gravity for
theentire body.

Answer 1

The location of the center of gravity for the entire body, relative to the floor is 1.03 m

Step-by-step explanation:

To find the center of gravity of a system of particles, we use that

`R_(cog) = (r_(1)*m_(1)+r_(2)*m_(2)+...+r_(n)*m_(n))/(M)`

where R is the vector center of gravity of the system, formed by n particles, and n masses.

In this case, for a person standing on the floor and being their body divided in three sectors, each one with a weight and an altitud in a specific point (center of gravity of the body sector), instead of mass we have every "particle" weight in Newtons (force instead of mass), being each "particle" in the formula, a sector of the body.

On the other hand, we use only magnitude for the calculation, because the gravity force is vertical to the floor, so instead of our vector formula, we use it in the vertical direction as a magnitude formula. Thus

`Y_(cog) = (y_(1)*W_(1)+y_(2)*W_(2)+y_(3)*W_(3))/(Wt)`

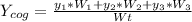
where Y is the center of gravity, y=1, 2, 3 is every "sector point" altitude from the floor, W=1, 2, 3 is every weight of a body "sector", and Wt is the sum of the three weights.

In this way we replace in our formula with the correspondent values

`Y_(cog) = (1.28m*438N+0.76m*144N+0.25m*87N)/(669N)`

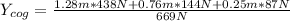
obtaining our result

`Y_(cog)=1.03 m`