Question

A closed, rigid, 0.50 m^3 tank is filled with 12 kg of water. The initial pressure is p1 = 20 bar. The water is cooled until the pressure is P2 = 4 bar. Determine the initial quality, X1, and the heat transfer, in kJ.

Answer 1

X1= 41%

heat transfer = -3450.676 KJ

Step-by-step explanation:

To get the properties for pure substance in a system we need to know at least to properties. These are usually pressure and temperature because they’re easy to measure. In this case we know the initial pressure (20 bar) which is not enough to get all the properties, but they ask to determine quality, this a property that just have meaning in the two-phase region (equilibrium) so with this information we can get the temperature of the system and all its properties.

There is another property that we can calculate from the data. This is the specific volume. This is defined as
`(volume)/(mass)`. We know the mass (12 Kg) and we can assume the volume is the volume of the tank (0.5
`m^(3)`) because they say that the tank was filled.

With this we get a specific volume of

Specific volume =
`(0,5 m^(3))/( 12 kg)= 0.04166667 (m^(3))/(Kg)`

From the thermodynamic tables we can get the data for the saturated region with a pressure of 20 bar.

Temperature of saturation = 212.385 °C

Specific volume for the saturated steam (vg) = 0.0995805

`X =((0.04166667- 0.00117675))/( (0.0995805 – 0.00117675)) = 0.411`

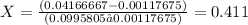
The quality is 41%

To calculate the heat transfer we use the next equation.

Q = m * Cp * delta T

Where

Q = heat transfer (Joules, J)

m= mass of the substance (g)

Cp = specific heat (J/g*K) from tables

Delta T = change in temperature in K for this equation.

The mass of the substance is 12 kg or 12000 g for this equation

Cp from tables is 4,1813 J/g*K. You can find this value for water in different states. Here we are using the value for liquid water.

For delta T, we know the initial temperature 212.385 °C.

We also know that the system was cooled. Since we don’t have more information, we can assume that the system was cooled until a condition where all the steam condensates so now we have a saturated liquid. Since we know the pressure (4 bar), we can get the temperature of saturation for this condition from the thermodynamics tables. This is 143.613 °C, so this is the final temperature for the system.

T(K) = T°C +273

T1(K) = 212.385 + 273.15 = 485.535 K

T2 (K) = 143.613 +273.15= 416.763 K

Delta T (K) = (T2-T1) =416.763 K - 485.535 K = -68.772 K

Now we can calculate Q

Q = 12000g * 4,1813 J/g*K* (-68.772 K) = -3450676.36 J or -3450.676 KJ

Is negative because the heat is transfer from the water to the surroundings