Question

For a normal distribution with mean equal to - 30 and standard deviation equal to 9 What is the area under the curve that is between - 34.5 and - 39.

Answer 1

Answer: 0.1498 square units.

Explanation:

Let x be any random variable that follows normal distribution.

Given : For a normal distribution with mean equal to - 30 and standard deviation equal to 9.

i.e.
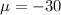`\mu=-30` and
`\sigma=9`

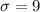
Use formula
`z=(x-\mu)/(\sigma)` to find the z-value corresponds to -34.5 will be

`z=(-34.5-(-30))/(9)=(-34.5+30)/(9)=(-4.5)/(9)=-0.5`

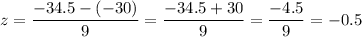
Similarly, the z-value corresponds to -38 will be

`z=(-39-(-30))/(9)=(-39+30)/(9)=(-9)/(9)=-1`

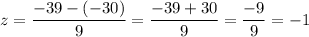
By using the standard normal table for z-values , we have

The area under the curve that is between - 34.5 and - 39. will be :-

`P(-1<z<-0.5)=P(z<-0.5)-P(z<-1)\\\\=(1-P(z<0.5))-(1-P(z<1))\\\\=1-P(z<0.5)-1+P(z<1)\\\\=P(z<1)-P(z<0.5)\\\\=0.8413-0.6915=0.1498`

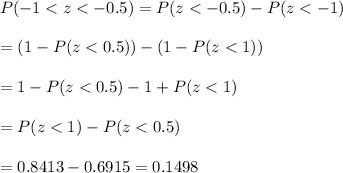
Hence, the area under the curve that is between - 34.5 and - 39 = 0.1498 square units.