Answer: 0.0011
Explanation:
By using the standard normal distribution table , the probability that Z is to the left of 3.05 is
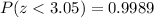
We know that the probability that Z is to the right of z is given by :-
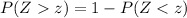
Similarly, the probability that Z is to the right of 3.05 will be :-
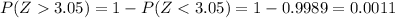
Hence, the probability that Z is to the right of 3.05 = 0.0011