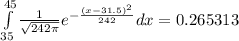Question

For a normal distribution with mean equal to 31.5 and standard deviation equal to 11, what is the area under the curve that is between 35 and 45?

Answer 1

The area is given by the following integral:
`\int\limits^(45)_(35) (1)/(√(242\pi))e^{-((x-31.5)^2)/(242)} dx`, which can be approximated by: 0.265313

Explanation:

A normal distribution is defined as:

`f(x)=(1)/(√(2\pi \sigma^2))e^{-((x-\mu)^2)/(2\sigma^2)}`

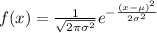
, where the greek letter sigma stands for the standard deviation and mu for the mean. Since in our problem we have a mean = 31.5 and a standard deviation = 11, then we can write this function as:

`f(x)=(1)/(√(242\pi))e^{-((x-31.5)^2)/(242)}`

Now, we need to find the area below this function, between 35 and 45, and in order to do this, we need to integrate the function. The normal distribution does not has an exact closed form integral, therefore we will have to solve the integral in a software that allows for numerical calculations (I used the online software Wolfram|Alpha).

`\int\limits^(45)_(35) (1)/(√(242\pi))e^{-((x-31.5)^2)/(242)} dx =0.265313`