Question

Population mean = 80

standard deviation = 20
sample = 60
What is the probability that the sample mean will be between84
and 88?

Answer 1

The answer is : 0.0597

Explanation:

Population mean = μ = 80

Standard deviation = σ = 20

Sample = N = 60

σ_mean = σ/√N

= (20)/√(60) = 2.582

Now we will find z1 and z2.

z1 = {(84) - μ}/σ_mean =
`{(84)-(80)}/(2.582)= 1.549`

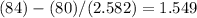
z2 = {(88) - μ}/σ_mean =
`{(88)-(80)}/(2.582)= 3.098`

Now probability that the sample mean will be between 84 and 88 is given by:

Prob{ (1.549) ≤ Z≤ (3.098) } = (0.9990) -(0.9393) = 0.0597