Answer:
The basis for the null space of A is
![{\left[\begin{array}{c}-1&-1&1&0\end{array}\right],\left[\begin{array}{c}-1&1&0&1\end{array}\right]}](https://img.qammunity.org/2020/formulas/mathematics/college/gtith5244wd0akqymkh8ajr8bpfjn4i68h.png)
Explanation:
- The first step is to find the reduced row echelon form of the matrix:
![\left[\begin{array}{cccc}1&0&1&1\\3&2&5&1\\0&4&4&-4\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/ze7jce3yscjwysk30gx516t6uezo7d5bwu.png)
- Make zeros in column 1 except the entry at row 1, column 1. Subtract row 1 multiplied by 3 from row 2
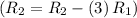
![\left[\begin{array}{cccc}1&0&1&1\\0&2&2&-2\\0&4&4&-4\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/z9jqml6yglzw1z6ftob3t5ztl1i7ygjjno.png)
- Make zeros in column 2 except the entry at row 2, column 2. Subtract row 2 multiplied by 2 from row 3
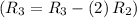
![\left[\begin{array}{cccc}1&0&1&1\\0&2&2&-2\\0&0&0&0\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/p2irwvo1br3f6zhp96y9g8hrfe1t4m1ehb.png)
- Multiply the second row by 1/2
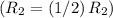
![\left[\begin{array}{cccc}1&0&1&1\\0&1&1&-1\\0&0&0&0\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/d6egdqfx16rcrisjlm6ncpgxciqamgtdqw.png)
2. Convert the matrix equation back to an equivalent system and solve the matrix equation
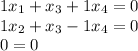
![\left[\begin{array}{cccc}1&0&1&1\\0&1&1&-1\\0&0&0&0\end{array}\right] \left[\begin{array}{c}x_(1) &x_(2) &x_(3)&x_(4) \end{array}\right]=\left[\begin{array}{c}0&0&0\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/m50yohwk9emj03wpxm7ghpoek4n9u7685o.png)
If we take
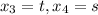 then
then
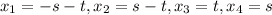
Therefore,
![\boldsymbol{x}=\left[\begin{array}{c}-s-t&s-t&t&s\end{array}\right]=\left[\begin{array}{c}-1&-1&1&0\end{array}\right]t+\left[\begin{array}{c}-1&1&0&1\end{array}\right]s\\\boldsymbol{x}=\left[\begin{array}{c}-1&-1&1&0\end{array}\right]x_(3) +\left[\begin{array}{c}-1&1&0&1\end{array}\right]x_(4)](https://img.qammunity.org/2020/formulas/mathematics/college/sjrn2hjwiawrvrb8gipiprweswo6n7qdsc.png)
The null space has a basis formed by the set {
![{\left[\begin{array}{c}-1&-1&1&0\end{array}\right],\left[\begin{array}{c}-1&1&0&1\end{array}\right]}](https://img.qammunity.org/2020/formulas/mathematics/college/gtith5244wd0akqymkh8ajr8bpfjn4i68h.png) }
}