Question

The American Sugar Producers Association wants to estimate

themean yearly sugar consumption. A sample of n = 12 people
revealsthe mean yearly consuption to be 55 pounds with a
standarddeviation of 20 pounds. Find the lower bound for the 98%
confidenceinterval for the mean yearly sugar consumption. Assume
thepopulation is normal.

Answer 1

Answer: 39.308 pounds

Explanation:

We assume that the given population is normally distributed.

Given : Significance level :
`\alpha: 1-0.98=0.02`

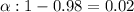
Sample size : n= 12, which is small sample (n<30), so we use t-test.

Critical value (by using the t-value table)=
`t_(n-1, \alpha/2)=t_(11,0.01)=2.718`

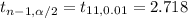
Sample mean :
`\overline{x}=50`

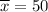
Standard deviation :
`\sigma= 20`

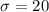
The lower bound of confidence interval is given by :-

`\overline{x}-t_((n-1,\alpha/2))(\sigma)/(√(n))`

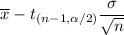
i.e.
`55-(2.718)(20)/(√(12))`

`=55-15.6923803166\approx55-15.692=39.308`

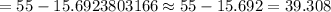
Hence, the lower bound for the 98% confidence interval for the mean yearly sugar consumption= 39.308 pounds