Answer:
The solution of given equation are -1 and 5.
Explanation:
The given equation is
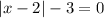
We need to solve the above equation by finding the zeros of
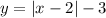
The vertex form of an absolute function is
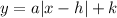
where, a is constant and (h,k) is vertex.
Here, h=2, k=-3. So vertex of the function is (2,-3).
The table of values is
x y
0 -1
2 -3
4 -1
Plot these points on a coordinate plane and draw a V-shaped curve with vertex at (2,-3).
From the given graph it is clear that the graph intersect x-axis at -1 and 5. So, zeroes of the function y=|x-2|-3 are -1 and 5.
Therefore the solution of given equation are -1 and 5.
Now solve the given equation algebraically.
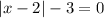
Add 3 on both sides.
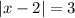
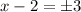
Add 2 on both sides.
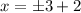
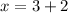 and
and
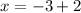
 and
and

Therefore the solution of given equation are -1 and 5.