Answer:
The velocity of flow in 10in pipe is 4.16 ft/s.
Step-by-step explanation:
Given that
Specific gravity = 0.8
Viscosity =0.00042
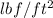
For pipe 1
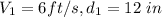
For pipe 1
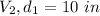
If we assume that flow in the both pipe is laminar
For laminar flow through circular pipe
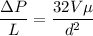
So same pressure drop we can say that
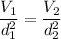
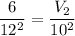
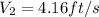
So the velocity of flow in 10in pipe is 4.16 ft/s.