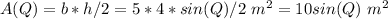Question

Two sides of a triangle are 4 m and 5 m in length. Express the area A of the triangle in terms of the angle Q between these two sides.

Answer 1

The area of the triangle, as a function of the angle between the two given sides, is:
`A(Q) = 10sin(Q)\ m^(2)`

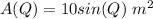
Explanation:

We know that the area of a triangle is given by the formula A = b*h/2, where b stands for the base and h for the height.

In our problem, we can choose anyone of them as the base. Let us choose, for example, b = 5 m. Now that we know the value of the base, we can use the value of the other side (4 m) and the angle between these two sides (Q) to calculate the height:

`h = (4 m)sin(Q)`

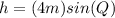
Therefore, the are of the triangle, as a function of the angle between these two sides is:

`A(Q) = b*h/2 =5*4*sin(Q)/2\ m^(2) = 10sin(Q)\ m^(2)`