Answer:
factor of safety for A36 structural steel is 0.82
Step-by-step explanation:
given data:
side of column = 3.5 inches
wall thickness = 0.225 inches
load P = 22 kip
Length od column = 9 ft
we know that critical stress is given as

where
r is radius of gyration
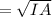
Here I is moment od inertia
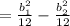

For hollow steel area is given as

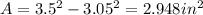
critical stress

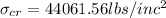
considering Structural steel A36
so A36
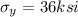
factor of safety
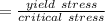
factor of safety =
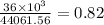
factor of safety for A36 structural steel is 0.82