Question

The specific reaction rate of a reaction at 492k is 2.46 second inverse and at 528k 47.5 second inverse.find activation energy and ko.

Answer 1

Ea = 177x10³ J/mol

ko =
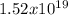`1.52x10^(19)` J/mol

Step-by-step explanation:

The specific reaction rate can be calculated by Arrhenius equation:

`k = koxe^(-Ea/RT)`

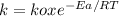
Where k0 is a constant, Ea is the activation energy, R is the gas constant, and T the temperature in Kelvin.

k depends on the temperature, so, we can divide the k of two different temperatures:

`(k1)/(k2) = (koxe^(-Ea/RT1))/(koxe^(-Ea/RT2))`

`(k1)/(k2) = e^(-Ea/RT1 + Ea/RT2)`

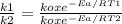
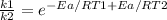
Applying natural logathim in both sides of the equations:

ln(k1/k2) = Ea/RT2 - Ea/RT1

ln(k1/k2) = (Ea/R)x(1/T2 - 1/T1)

R = 8.314 J/mol.K

ln(2.46/47.5) = (Ea/8.314)x(1/528 - 1/492)

ln(0.052) = (Ea/8.314)x(-1.38x
`10^(-4)`

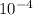
-1.67x
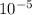`10^(-5)`xEa = -2.95

Ea = 177x10³ J/mol

To find ko, we just need to substitute Ea in one of the specific reaction rate equation:

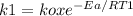
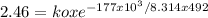
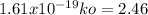
`k1 = koxe^(-Ea/RT1)`

`2.46 = koxe^(-177x10^3/8.314x492)`

`1.61x10^(-19)ko = 2.46`

ko =
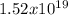`1.52x10^(19)` J/mol