Question

Two point charges of -7uC and 4uC are a distance of 20

cmapart. How much work does it take to move these charges outto a
separation of 90 cm apart @ a constant speed?

Answer 1

Answer is c

Step-by-step explanation:

trust me.

Answer 2

Approximately 0.979 J.

Step-by-step explanation:

Assume that the two charges are in vacuum. Apply the coulomb's law to find their initial and final electrical potential energy
`\mathrm{EPE}`.

`\displaystyle \mathrm{EPE} = (k \cdot q_1 \cdot q_2)/(r)`,

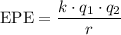where

• The coulomb's constant
  `k = 8.99* 10^(9)\; \rm N\cdot m^(2) \cdot C^(-2)`,
• 
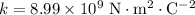  `q_1` and
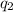  `q_2` are the sizes of the two charges, and
• 
  `r` is the separation of (the center of) the two charges.

Note that there's no negative sign before the fraction.

Make sure that all values are in SI units:

• 
  `q_1 = -7\rm \;\mu C = -7* 10^(-6)\; C`;
• 
  `q_2 = 4\rm \;\mu C = 4* 10^(-6)\; C`;

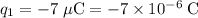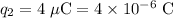• Initial separation:
  `\rm 20\; cm = 0.20\; cm`;
• Final separation:
  `\rm 90\; cm = 0.90\; cm`.

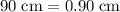Apply Coulomb's law:

Initial potential energy:

`\begin{aligned} (k \cdot q_1 \cdot q_2)/(r) &= (8.99* 10^(9)* (-7* 10^(-6))* 4* 10^(-6))/(0.20)\\&= \rm -1.2586\; J\end{aligned}`.

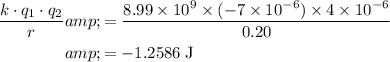Final potential energy:

`\begin{aligned} (k \cdot q_1 \cdot q_2)/(r) &= (8.99* 10^(9)* (-7* 10^(-6))* 4* 10^(-6))/(0.90)\\&= \rm -0.279689\; J\end{aligned}`.

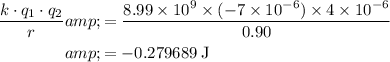The final potential energy is less negative than the initial one. In other words, the two particles gain energy in this process. The energy difference (final minus initial) will be equal to the work required to move them at a constant speed.

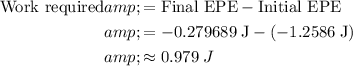`\begin{aligned}\text{Work required} &= \text{Final EPE} - \text{Initial EPE}\\&= \rm  -0.279689\; J - (-1.2586\; J)\\&\approx 0.979\; J\end{aligned}`.