Question

What is the boiling point of an aqueuous solution of

anonelectrolyte that has an osmotic pressure of 10.50 atm at 25C?
Kbof water is 0.52C/m. Assume its density is the same as
purewater.

Answer 1

100.223°C is the boiling point of an aqueous solution.

Step-by-step explanation:

Osmotic pressure of the solution = π = 10.50 atm

Temperature of the solution =T= 25 °C = 298 .15 K

Concentration of the solution = c

van'y Hoff factor = i = 1 (non electrolyte)

`\pi =icRT`

`c=(\pi )/(RT)=(10.50 atm)/(0.0821 atm L/mol K* 298.15 K)`

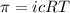
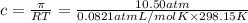
c = 0.429 mol/L = 0.429 mol/kg = m

(density of solution is the same as pure water)

m = molality of the solution

Elevation in boiling point =
`\Delta T_b`

`\Delta T_b=iK_b* m`

`\Delta T_b=T_b-T`

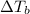
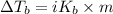
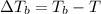
T = Boiling point of the pure solvent

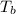`T_b` = boiling point of the solution

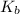`K_b` = Molal elevation constant

We have :

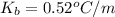`K_b=0.52^oC/m` (given)

m = 0.429 mol/kg

T = 100° C (water)

`\Delta T_b=1* 0.52^oC/m* 0.429 mol/kg`

`\Delta T_b=0.223^oC`

`\Delta T_b=T_b-T`

`T_b=\Delta T_b+T=0.223^oC+100^oC=100.223^oC`

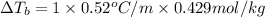
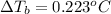
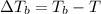
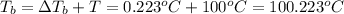
100.223°C is the boiling point of an aqueous solution.