Question

Solve the lenear system by using the inverse of the coefficient matrix:

x + 2z = -1
2x - y = 2
3y + 4z = 1

Answer 1

The solution of this system is x=9/4, y=5/2, and z=-13/8

Explanation:

1. Writing the equations in matrix form

The system of linear equations given can be written in matrix form as

`\left[\begin{array}{ccc}1&0&2\\2&-1&0\\0&3&4\end{array}\right]\left[\begin{array}{c}x&y&z\end{array}\right] = \left[\begin{array}{c}-1&2&1\end{array}\right]`

Writing

A =
`\left[\begin{array}{ccc}1&0&2\\2&-1&0\\0&3&4\end{array}\right]`

X =
`\left[\begin{array}{c}x&y&z\end{array}\right]`

B =
`\left[\begin{array}{c}-1&2&1\end{array}\right]`

we have

AX=B

This is the matrix form of the simultaneous equations.

2. Solving the simultaneous equations

Given

AX=B

we can multiply both sides by the inverse of A

`A^(-1)AX=A^(-1)B`

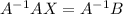
We know that
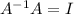`A^(-1)A=I`, the identity matrix, so

`X=A^(-1)B`

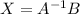
All we need to do is calculate the inverse of the matrix of coefficients, and finally perform matrix multiplication.

3. Calculate the inverse of the matrix of coefficients

A =
`\left[\begin{array}{ccc}1&0&2\\2&-1&0\\0&3&4\end{array}\right]`

To find the inverse matrix, augment it with the identity matrix and perform row operations trying to make the identity matrix to the left. Then to the right will be inverse matrix.

`\left[\begin{array}ccc1&0&2&1&0&0\\2&-1&0&0&1&0\\0&3&4&0&0&1\end{array}\right]`

• Make zeros in column 1 except the entry at row 1, column 1. Subtract row 1 multiplied by 2 from row 2

`\left[\begin{array}ccc1&0&2&1&0&0\\0&-1&-4&-2&1&0\\0&3&4&0&0&1\end{array}\right]`

• Make zeros in column 2 except the entry at row 2, column 2. Add row 2 multiplied by 3 to row 3

`\left[\begin{array}ccc1&0&2&1&0&0\\0&-1&-4&-2&1&0\\0&0&-8&-6&3&1\end{array}\right]`

• Multiply row 2 by −1

`\left[\begin{array}ccc1&0&2&1&0&0\\0&1&4&2&-1&0\\0&0&-8&-6&3&1\end{array}\right]`

• Make zeros in column 3 except the entry at row 3, column 3. Divide row 3 by −8

`\left[\begin{array}ccc1&0&2&1&0&0\\0&1&4&2&-1&0\\0&0&1&3/4&-3/8&-1/8\end{array}\right]`

• Subtract row 3 multiplied by 2 from row 1

`\left[\begin{array}ccc1&0&0&-1/2&3/4&1/4\\0&1&4&2&-1&0\\0&0&1&3/4&-3/8&-1/8\end{array}\right]`

• Subtract row 3 multiplied by 4 from row 2

`\left[\begin{array}ccc1&0&0&-1/2&3/4&1/4\\0&1&0&-1&1/2&1/2\\0&0&1&3/4&-3/8&-1/8\end{array}\right]`

As can be seen, we have obtained the identity matrix to the left. So, we are done.

`A^(-1) = \left[\begin{array}{ccc}-1/2&3/4&1/4\\-1&1/2&1/2\\3/4&-3/8&-1/8\end{array}\right]`

4. Find the solution
`X=A^(-1)B`

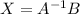
`X= \left[\begin{array}{ccc}-1/2&3/4&1/4\\-1&1/2&1/2\\3/4&-3/8&-1/8\end{array}\right]\cdot \left[\begin{array}{c}-1&2&1\end{array}\right] = \left[\begin{array}{c}9/4&5/2&-13/8\end{array}\right]`