Question

A 0.350kg bead slides on a curved fritionless wire,

startingfrom rest at point A. At point B the bead
collideselastically with a 0.530kg ball at rest. find distance call
risesas it moves up the wire. Point A is 2.20 m from ground andfree
fall accel is 9.80 m/s. round answer to 3 significantfigures.

Answer 1

h2 = 0.092m

Step-by-step explanation:

From a balance of energy from point A to point B, we get speed before the collision:

`m1*g*h-(m1*V_B^2)/(2)=0` Solving for Vb:

`V_B=√(2gh)=6.56658m/s`

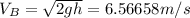
Since the collision is elastic, we now that velocity of bead 1 after the collision is given by:

`V_(B')=V_B*(m1-m2)/(m1+m2) = √(2gh)* (m1-m2)/(m1+m2)=-1.34316m/s`

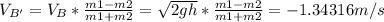
Now, by doing another balance of energy from the instant after the collision, to the point where bead 1 stops, we get the distance it rises:

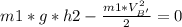`m1*g*h2-(m1*V_(B')^2)/(2)=0` Solving for h2:

h2 = 0.092m