1 Answer

CoreyRS · Answer 1 · 2020-11-10T13:28:37+0000

I assume the first equation is supposed to be

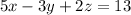
5x-3y+2z=13

and not

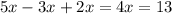
5x-3x+2x=4x=13

As an augmented matrix, this system is given by

$\left[\begin{array}ccc5&-3&2&13\\2&-1&-3&1\\4&-2&4&12\end{array}\right]$

Multiply through row 3 by 1/2:

$\left[\begin{array}ccc5&-3&2&13\\2&-1&-3&1\\2&-1&2&6\end{array}\right]$

Add -1(row 2) to row 3:

$\left[\begin{array}ccc5&-3&2&13\\2&-1&-3&1\\0&0&5&5\end{array}\right]$

Multiply through row 3 by 1/5:

$\left[\begin{array}c5&-3&2&13\\2&-1&-3&1\\0&0&1&1\end{array}\right]$

Add -2(row 3) to row 1, and add 3(row 3) to row 2:

$\left[\begin{array}c5&-3&0&11\\2&-1&0&4\\0&0&1&1\end{array}\right]$

Add -3(row 2) to row 1:

$\left[\begin{array}ccc-1&0&0&-1\\2&-1&0&4\\0&0&1&1\end{array}\right]$

Multiply through row 1 by -1:

$\left[\begin{array}ccc1&0&0&1\\2&-1&0&4\\0&0&1&1\end{array}\right]$

Add -2(row 1) to row 2:

$\left[\begin{array}ccc1&0&0&1\\0&-1&0&2\\0&0&1&1\end{array}\right]$

Multipy through row 2 by -1:

$\left[\begin{array}c1&0&0&1\\0&1&0&-2\\0&0&1&1\end{array}\right]$

The solution to the system is then

$\boxed{x=1,y=-2,z=1}$

Please log in or register to add a comment.