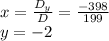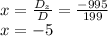Answer:
The solution to the system is
 ,
,
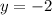 and
and
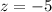
Explanation:
Cramer's rule defines the solution of a system of equations in the following way:
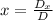 ,
,
 and
and
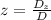 where
where
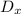 ,
,
 and
and
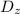 are the determinants formed by replacing the x,y and z-column values with the answer-column values respectively.
are the determinants formed by replacing the x,y and z-column values with the answer-column values respectively.
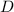 is the determinant of the system. Let's see how this rule applies to this system.
is the determinant of the system. Let's see how this rule applies to this system.
The system can be written in matrix form like:
![\left[\begin{array}{ccc}5&-3&1\\0&2&-3\\7&10&0\end{array}\right]* \left[\begin{array}{c}x&y&z\end{array}\right] = \left[\begin{array}{c}6&11&-13\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/qsbo63sqscckhblndz0u0rph94lfmqadhl.png)
Then each of the previous determinants are given by:
 Notice how the x-column has been substituted with the answer-column one.
Notice how the x-column has been substituted with the answer-column one.
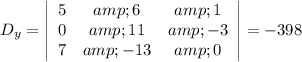 Notice how the y-column has been substituted with the answer-column one.
Notice how the y-column has been substituted with the answer-column one.
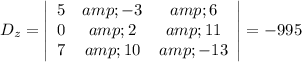
Then, substituting the values: