Question

Programming (Optimizing an Objective Function) A manufacturer of ski clothing makes ski pants and ski jackets. The profit on a pair of ski pants is $2.00 and the profit on a jacket is $1.50. Both pants and jackets require the work of sewing operators and cutters. There are 60 minutes of sewing operator time and 48 minutes of cutter time available. It takes 8 minutes to sew one pair of ski pants and 4 minutes to sew one jacket. Cutters take 4 minutes on pants and 8 minutes on a jacket. Find the number of pants and jackets the manufacturer should make in order to maximize the profit pairs of pants jackets

Answer 1

In order to maximize the profit pairs of pants jackets, the manufactures should make 6 pants and 3 jackets.

Explanation:

This problem can be solved by a system of first order equations:

I am going to say that
`x` is the number of pants and
`y` is the number of jackets that the manufacturer should make.

The profit will be maximized when all the avaiable time of the sewing operator and the cutter time has been used.

The problem states that there are 60 minutes of sewing operator time available. It takes 8 minutes to sew one pair of ski pants and 4 minutes to sew one jacket. So:

`8x + 4y = 60`

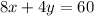
We can simplify this equation by 4. So:

`2x + y = 15`

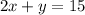
The problem also states that there are 48 minutes of cutter time available. Cutters take 4 minutes on pants and 8 minutes on a jacket. So:

`4x + 8y = 48`

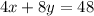
Again simplifying by 4,

`x + 2y = 12`.

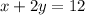Now we have to solve the following system:

`2x + y = 15`

`x + 2y = 12`

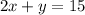
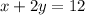
I am going to write y as a function of x in the first equation, and replace it in the second.

`y = 15 - 2x`

`x + 2y = 12`

`x + 2(15 - 2x) = 12`

`x + 30 - 4x = 12`

`-3x = -18`

`3x = 18`

`x = (18)/(3)`

`x = 6`

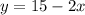
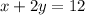
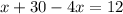
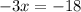
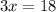
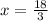
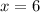
Now, replacing

`y = 15 - 2x = 15 - 2(6) = 15 - 12 = 3`

In order to maximize the profit pairs of pants jackets, the manufactures should make 6 pants and 3 jackets.