Question

Social Sciences Alcohol Abstinence The Harvard School of Public Health completed a study on alcohol consumption on college campuses. They concluded that 20.7% of women attending all-women colleges abstained from alcohol, compared to e6% of women attending coeducational colleges. Approximately 4.7% of women college students attend all-women schools. Source: Harvard School of Public Health. (a) What is the probability that a randomly selected female student abstains from alcohol? (b) If a randomly selected female student abstains from alcohol, what is the probability she attends a coedücational colege?

Answer 1

a) There is a 6.69% probability that a randomly selected female student abstains from alcohol.

b) If a randomly selected female student abstains from alcohol, there is a 82.87% probability that she attends a coeducational college.

Explanation:

This is a probability problem:

We have these following probabilities:

-20.7% of a woman attending an all-women college abstaining from alcohol.

-6% of a woman attending a coeducational college abstaining from alcohol.

-4.7% of a woman attending an all-women college

- 100%-4.7% = 95.3% of a woman attending a coeducational college.

(a) What is the probability that a randomly selected female student abstains from alcohol?

`P = P_(1) + P_(2)`

`P_(1)` is the probability of a woman attending an all-women college being chosen and abstaining from alcohol. There is a 0.047 probability of a woman attending an all-women college being chosen and a 0.207 probability that she abstain from alcohol. So:

`P_(1) = 0.047*0.207 = 0.009729`

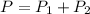
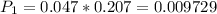
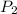`P_(2)` is the probability of a woman attending a coeducational college being chosen and abstaining from alcohol. There is a 0.953 probability of a woman attending a coeducational college being chosen and a 0.06 probability that she abstain from alcohol. So:

`P_(2) = 0.953*0.06 = 0.05718`

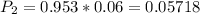
So, the probability of a randomly selected female student abstaining from alcohol is:

`P = P_(1) + P_(2) = 0.009729 + 0.05718 = 0.0669`

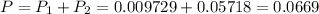
There is a 6.69% probability that a randomly selected female student abstains from alcohol.

(b) If a randomly selected female student abstains from alcohol, what is the probability she attends a coedücational colege?

This can be formulated as the following problem:

What is the probability of B happening, knowing that A has happened.

Here:

What is the probability of a woman attending a coeducational college, knowing that she abstains from alcohol.

It can be calculated by the following formula:

`P = (P(B).P(A/B))/(P(A))`

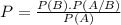
Where P(B) is the probability of B happening, P(A/B) is the probability of A happening knowing that B happened and P(A) is the probability of A happening.

We have the following probabilities:

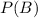`P(B)` is the probability of a woman from a coeducational college being chosen. So
`P(B) = 0.953`

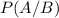`P(A/B)` is the probability of a woman abstaining from alcohol, given that she attends a coeducational college. So
`P(A/B) = 0.06`

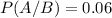
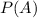`P(A)` is the probability of a woman abstaining from alcohol. From a),
`P(A) = 0.0669`

So, the probability that a randomly selected female student attends a coeducational college, given that she abstains from alcohol is:

`P = (P(B).P(A/B))/(P(A)) = ((0.953)*(0.06))/((0.0669)) = 0.8287`

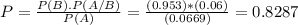
If a randomly selected female student abstains from alcohol, there is a 82.87% probability that she attends a coeducational college.