Question

Give the first three non-zero terms of the Taylor series for f(x) = tan(x) about x 0· Use this to approximate tan(1) and give an upper bound on the error in this approximation

Answer 1

`f(x)=x+(x^(3))/(3)+(2x^(4))/(3)....`

Approximate error = 0.4426

Explanation:

f(x)=tanx, a=0

Maclaurin series formula used is given below

`f(x)=\sum_(n=0)^(\infty)(f^((n))(0)x^(n))/(n!)=f(0)+f'(0)x+(f''(0))/(2!)x^(2)+(f'''(0))/(3!)x^(3)+....`

f(x)=tanx

f(0)=tan0=0

`f'(x)=sec^(2)x\\f'(0)=sec^(2)0=1\\f''(x)=2sec^(2)xtanx\\f''(0)=2sec^(2)0tan0=0\\f'''(x)=-4sec^(2)x+6sec^(4)x\\f'''(0)=-4sec^(2)0+6sec^(4)0=-4+6=2\\`

`f''''(x)=-8(2sec^(2)xtan^(2)x+sec^(4)x)+24(4sec^(4)xtan^(2)x)+sec^(6))\\f''''(0)=-8(0+1)+24(0+1)=-8+24=16\\`

`f(x)=0+x+0+(2x^(3))/(3!)+(16x^(4))/(4!)\\`

`f(x)=x+(x^(3))/(3)+(2x^(4))/(3)\\`

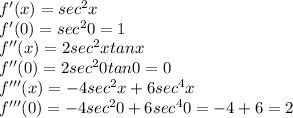
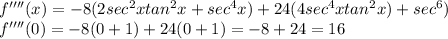
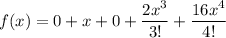
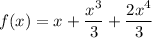
Hence, the Taylor series for f(x)=tanx is given by

`f(x)=x+(x^(3))/(3)+(2x^(4))/(3)....`

Maclaurin series upper bound error formula used is given as

R_n(x)=|f(x)-T_n(x)|

R_3(x)=|tanx-T_3(x)|

`R_3(x)=|tanx-x-(x^(3))/(3)-(2x^(4))/(3)|`

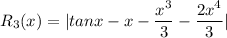
Plugging this value x=1

`R_3(x)=|tan(1)-1-(1)/(3)-(2)/(3)|\\`

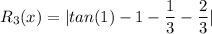
R_3(x)=|1.5574-1-0.333-0.666|

R_3(x)=|-0.4426|=0.4426

Hence, upper bound on the error approximation

tan(1)=0.4426