Question

A student club has seven members. 3 are to be chosen to go together to a national meeting. A) how many distinct groups of 3 can be chosen? B) if the student club contains 4 men and 3 women, how many distinct groups of 3 contain two men and one woman?

Answer 1

1) 35 distinct groups can be formed.

2) 18 distinct groups can be formed containing 2 men and 1 woman.

Explanation:

The no of groups of 3 members that can be chosen from 7 members equals no of combinations of 3 members that can be formed from 7 members.

Thus no of groups =

`n=\binom{7}{3}=(7!)/((7-3)!* 3!)=35`

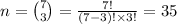
thus 35 distinct groups can be formed.

Part b)

Now since the condition is that we have to choose 2 men and 1 women to form the group

let A and B be men member's of group thus we have to choose 2 member's from a pool of 4 men which equals

`\binom{4}{2}=(4!)/((4-2)!* 2!)=6`

Let the Woman member be C thus we have to choose one woman from a pool of 3 women hence number of ways in which it can be done equals 3.

thus the group can be formed in
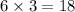`6* 3=18` different ways.