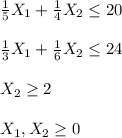Question

A company can use two workers to manufacture product 1 and product 2 during a business slowdown. Worker 1 will be available for 20 hours and worker 2 for 24 hours. Product 1 will require 5 hours of labor from worker 1 and 3 hours of specialized skill from worker 2. Product 2 will require 4 hours from worker 1 and 6 hours from worker 2. The finished products will contribute a net profit of $60 for product 1 and $50 for product 2. At least two units of product 2 must be manufactured to satisfy a contract requirement. Formulate a linear program to determine the profit maximizing course of action. (Hint: the simplest formulation assigns one decision variable to account for the number of units of product 1 to produce and the other decision variable to account for the number of units of product 2 to produce.)

Answer 1

The linear problem is to maximize
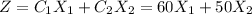`Z = C_ {1} X_ {1} + C_ {2}X_ {2} = 60X_ {1} + 50X_ {2}`, s.a.

subject to

`\frac {1} {5} X_ {1} + \frac {1} {4} X_ {2} \leq 20\\\\\frac {1} {3} X_ {1} + \frac {1} {6} X_ {2} \leq 24\\\\X_ {2} \geq 2\\\\X_ {1}, X_ {2} \geq 0`

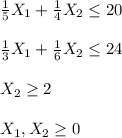
Explanation:

Let the decision variables be:

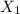`X_ {1}`: number of units of product 1 to produce.

`X_ {2}`: number of units of product 2 to produce.

Let the contributions be:

`C_ {1} = 60\\\\C_ {2} = 50`

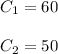
The objective function is:

`Z = C_(1) X_(1)+ C_(2)X_(2) = 60X_ {1} + 50X_ {2}`

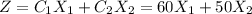
The restrictions are:

`\frac {1} {5} X_ {1} + \frac {1} {4} X_ {2} \leq 20\\\\\frac {1} {3} X_ {1} + \frac {1} {6} X_ {2} \leq 24\\\\X_ {2} \geq 2\\\\X_ {1}, X{2} \geq 2\\\\`

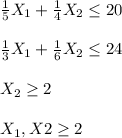
The linear problem is to maximize
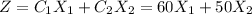`Z = C_ {1} X_ {1} + C_ {2}X_ {2} = 60X_ {1} + 50X_ {2}`, s.a.

subject to

`\frac {1} {5} X_ {1} + \frac {1} {4} X_ {2} \leq 20\\\\\frac {1} {3} X_ {1} + \frac {1} {6} X_ {2} \leq 24\\\\X_ {2} \geq 2\\\\X_ {1}, X_ {2} \geq 0`