Question

Mathematical induction of 3k-1 ≥ 4k ( 3k = k power of 3 )

Answer 1

For making mathematical induction, we need:

• a base case

An
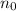`n_0` for which the relation holds true

• the induction step

if its true for
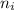`n_i`, then, is true for
`n_(i+1)`

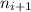
base case

the relationship is not true for 1 or 2

`1^3-1 = 0 < 4*1`

`2^3-1 = 8 -1 = 7 < 4*2 = 8`

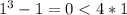
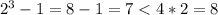
but, is true for 3

`3^3-1 = 27 -1 = 26 > 4*3 = 12`

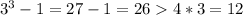
induction step

lets say that the relationship is true for n, this is

`n^3 -1 \ge 4 n`

lets add 4 on each side, this is

`n^3 -1 + 4 \ge 4 n + 4`

`n^3 + 3 \ge 4 (n + 1)`

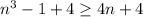
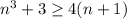
now

`(n+1)^3 = n^3 +3 n^2 + 3 n + 1`

`(n+1)^3 \ge n^3 + 3 n`

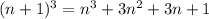
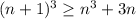
if
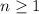`n \ge 1` then
`3 n \ge 3` , so

`(n+1)^3 \ge n^3 + 3 n \ge n^3 + 3`

`(n+1)^3 \ge  n^3 + 3 \ge 4 (n + 1)`

`(n+1)^3  \ge 4 (n + 1)`

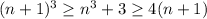
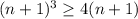
and this is what we were looking for!

So, for any natural equal or greater than 3, the relationship is true.