Question

A cannon fires a cannonball forward at a velocity of 48.1 m/s horizontally. If the cannon is on a mounted wagon 1.5 m tall, how far would the cannonball travel before it lands on the ground? (Show all work)

Answer 1

Answer: 473.640 m

Step-by-step explanation:

This situation is related to projectile motion or parabolic motion, in which the travel of the cannonball has two components: x-component and y-component. Being their main equations as follows:

x-component:

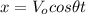`x=V_(o)cos\theta t` (1)

Where:

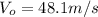`V_(o)=48.1 m/s` is the cannonball's initial velocity

`\theta=0` because we are told the cannonball is shot horizontally

`t` is the time since the cannonball is shot until it hits the ground

y-component:

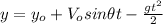`y=y_(o)+V_(o)sin\theta t-(gt^(2))/(2)` (2)

Where:

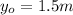`y_(o)=1.5m` is the initial height of the cannonball

`y=0` is the final height of the cannonball (when it finally hits the ground)

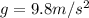`g=9.8m/s^(2)` is the acceleration due gravity

We need to find how far (horizontally) the cannonball has traveled before landing. This means we need to find the maximum distance in the x-component, let's call it
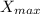`X_(max)` and this occurs when
`y=0`.

So, firstly we will find the time with (2):

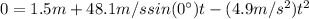`0=1.5 m+48. 1 m/s sin(0\°) t-(4.9 m/s^(2))t^2` (3)

Rearranging the equation:

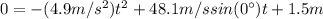`0=-(4.9 m/s^(2))t^2+48. 1 m/s sin(0\°) t+1.5 m` (4)

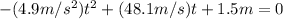`-(4.9 m/s^(2))t^2+(48. 1 m/s)  t+1.5 m=0` (5)

This is a quadratic equation (also called equation of the second degree) of the form
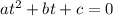`at^(2)+bt+c=0`, which can be solved with the following formula:

`t=\frac{-b \pm \sqrt{b^(2)-4ac}}{2a}` (6)

Where:

`a=-4.9 m/s^(2)`

`b=48.1 m/s`

`c=1.5 m`

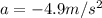
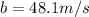
Substituting the known values:

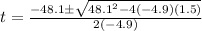`t=\frac{-48.1 \pm \sqrt{48.1^(2)-4(-4.9)(1.5)}}{2(-4.9)}` (7)

Solving (7) we find the positive result is:

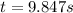`t=9.847 s` (8)

Substituting this value in (1):

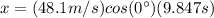`x=(48.1 m/s)cos(0\°) (9.847 s)` (9)

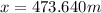`x=473.640 m` This is the horizontal distance the cannonball traveled before it landed on the ground.