Question

The total monthly profit for a firm is P(x)=6400x−18x^2− (1/3)x^3−40000 dollars, where x is the number of units sold. A maximum of 100 units can be sold per month.

How many units should be sold to maximize monthly profit? units

What is the maximum monthly profit when this number of units are sold? (Round your answer to the nearest whole number.) dollars

(Hint: When you solve for the critical values in this question, you'll have to solve a quadratic equation. You can do that using the quadratic formula, or you can do it by factoring.)

How to get this answer?

Answer 1

Maximum profits are earned when x = 64 that is when 64 units are sold.

Maximum Profit = P(64) = 2,08,490.666667$

Explanation:

We are given the following information:
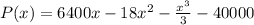`P(x) = 6400x - 18x^2 - (x^3)/(3) - 40000`, where P(x) is the profit function.

We will use double derivative test to find maximum profit.

Differentiating P(x) with respect to x and equating to zero, we get,

`\displaystyle(d(P(x)))/(dx) = 6400 - 36x - x^2`

Equating it to zero we get,

`x^2 + 36x - 6400 = 0`

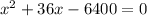
We use the quadratic formula to find the values of x:

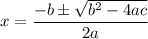`x = \displaystyle(-b \pm √(b^2 - 4ac) )/(2a)`, where a, b and c are coefficients of
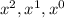`x^2, x^1 , x^0` respectively.

Putting these value we get x = -100, 64

Now, again differentiating

`\displaystyle(d^2(P(x)))/(dx^2) = -36 - 2x`

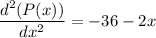
At x = 64,
`\displaystyle(d^2(P(x)))/(dx^2) < 0`

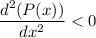
Hence, maxima occurs at x = 64.

Therefore, maximum profits are earned when x = 64 that is when 64 units are sold.

Maximum Profit = P(64) = 2,08,490.666667$