
Let
 , so that
, so that
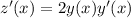 (which appears in the first term on the left side):
(which appears in the first term on the left side):
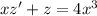
This ODE is linear in
 , and we don't have to find any integrating factor because the left side is already the derivative of a product:
, and we don't have to find any integrating factor because the left side is already the derivative of a product:
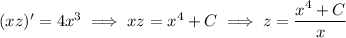
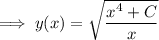
With
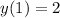 , we get
, we get
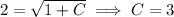
so the solution is as given in your post.