Question

Which terms are rational in the expansion of (\sqrt{3} + \frac{1}{\sqrt[4]{6}})^{15} . List the rational terms and justify why the others are not rational.

Answer 1

`(√(3) + \frac{1}{\sqrt[4]{6}})^(15)`

Binomial expansion formula,

`(a+b)^n=\sum_(r=0)^(n) ^nC_r (a)^(n-r) (b)^r`

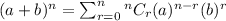
Where,

`^nC_r=(n!)/(r!(n-r)!)`

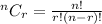
`\implies (√(3) + (1)/(2))^(15)=\sum_(r=0)^(15) ^(15)C_r (√(3))^(15-r) (\frac{1}{\sqrt[4]{6}})^r`

`=(√(3))^(15)+15(√(3))^(14)(\frac{1}{\sqrt[4]{6}})^1+105(√(3))^(13)(\frac{1}{\sqrt[4]{6}})^2+455(√(3))^(12)(\frac{1}{\sqrt[4]{6}})^3+1365(√(3))^(11)(\frac{1}{\sqrt[4]{6}})^4+3003(√(3))^(10)(\frac{1}{\sqrt[4]{6}})^5+5005(√(3))^(9)(\frac{1}{\sqrt[4]{6}})^6+6435(√(3))^(8)(\frac{1}{\sqrt[4]{6}})^7+6435(√(3))^(7)(\frac{1}{\sqrt[4]{6}})^8+5005(√(3))^(6)(\frac{1}{\sqrt[4]{6}})^9+3003(√(3))^(5)(\frac{1}{\sqrt[4]{6}})^(10)+1365(√(3))^(4)(\frac{1}{\sqrt[4]{6}})^(11)+455(√(3))^(3)(\frac{1}{\sqrt[4]{6}})^(12)+105(√(3))^(2)(\frac{1}{\sqrt[4]{6}})^(13)+15(√(3))^(1)(\frac{1}{\sqrt[4]{6}})^(14)+(\frac{1}{\sqrt[4]{6}})^(15)`

∵ both
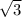`√(3)` and
`\frac{1}{\sqrt[4]{6}}` are irrational numbers,

And, if the power of √3 is even, it converted to a rational number,

If its power is odd it remained as irrational number,

But, the product of a rational number and irrational number is irrational,

Thus, all terms in the above expansion are irrational. ( which can not expressed in the form of p/q, where, p and q are integers s.t. q ≠ 0 )