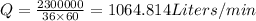Question

A 200 m3 swimming pool has been overly chlorinated by accidently

dumping an entire
container of chlorine, which amounted to 500 grams. This creates a
chlorine
concentration well in excess of the 0.20 mg/L that was the
objective at the time. With
which volumetric rate (in L/min) of freshwater should the pool be
flushed to decrease the
concentration to the desired level in 36 hours? You may assume the
chlorine does not
degrade chemically during those hours.

Answer 1

Water needs to be added into the pool at the rate of 1064.814 Liters/min.

Step-by-step explanation:

The concentration in mg/L of the chlorine in the pool that is induced by dumping the whole container of chlorine into the pool equals

`(500* 10^(3))/(200* 10^(3))=2.5mg/l`

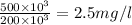
Since this is in excess to the required concentration of 0.20 mg/L

Let the amount of pure water we need to add be equal to 'V' liters now since pure water does not have any chlorine thus

By the conservation of mass principle we have

`0* V+2.5* 200* 10^(3)=0.20* (V+200* 10^(3))`

Solving for V we get

`V=(2.5* 200* 10^(3)-0.20* 200* 10^(3))/(0.20)=2300000Liters`

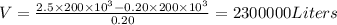
Thus 2300000 Liters of water needs to be further added in 36 hours

Thus the rate of flow in L/min equals

`Q=(2300000)/(36* 60)=1064.814Liters/min`