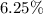Answer:
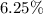
Explanation:
Given: A pharmacist attempts to weigh 0.375 g of morphine sulfate on a balance of dubious accuracy. When checked on a highly accurate balance, the weight is found to be 0.400 g.
i.e. Estimated weight = 0.375 g and Actual weight = 0.400 g
Now, the percentage of error in the first weighing is given by :-

Hence, the percentage of error in the first weighing =