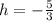Question

Determine the value (or values) of h such that the matrix: 2 - 3 h - 6 9 5 is the augmented matrix of a consistent linear system.

Answer 1

In order to have a consistent linear system represented by the augmented matrix:

`\left[\begin{array}{ccc}2&-3&h\\-6&9&5\end{array}\right]`

the value of h must be:

`h=-(5)/(3)`

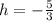
Explanation:

A system is consistent if it has a solution, this solution can be unique or a set of infinite solutions.

First, you take the augmented matrix and find the equivalent row echelon form using Gaussian-Jordan elimination:

To do this, you have to multiply the 1st row by 3 and add it to the 2nd row, the resulting matrix is:

`\left[\begin{array}{ccc}2&-3&h\\0&0&5+3h\end{array}\right]`

Now, write the system of equations:

`2x_1-3x_2=h\\0x_1+0x_2=5+3h`

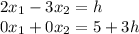
The only way this system has a solution is if 5+3h=0, then, to satisfy this, the value of h must be:

`h=-(5)/(3)`