Answer:
Intersection of collection of any closed set is a closed set.
Explanation:
Let F be a collection of arbitrary closed sets and let
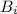 be closed set belonging to F.
be closed set belonging to F.
We define a closed set as the set that contains its limit point or in other words it can be described that the complement or not of a closed set is an open set.
Thus, we can write R as
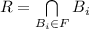
Now, applying De-Morgan's Theorem, we have
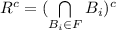
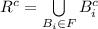
Since we knew
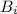 are closed set, thus,
are closed set, thus,
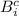 is an open set.
is an open set.
We also know that union of all open set is an open set.
Thus,
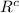 is an open set.
is an open set.
Thus, R is a closed set.
Hence, the theorem.