Answer:
248.79 ft
Explanation:
A projectile is fired from a cliff 220 ft above water at an inclination of 45 degrees to the horizontal, with a muzzle velocity of 65 ft per second.
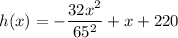
For maximum value of x, h(x)≥0

Solve quadratic equation for x
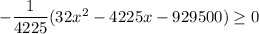
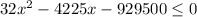
Using quadratic formula,
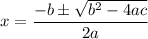
where, a=32, b=-4225, c=-929500
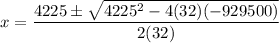
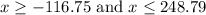
Hence, The maximum value of x will be 248.79 ft