Question

In how many ways can the digits 0,1,2,3,4,5,6,7,8,9 be arranged so that no prime number is in its original position?

I get the answer 1348225 by subtracting the number of derangements with fixed points 4,3,2 and 1 from 10! (the number of ways to arrange the numbers with none fixed).

Answer 1

Answer: 2399760

Explanation:

The concept we use here is Partial derangement.

It says that for m things , the number of ways to arrange them such that k things are not in their fixed position is given by :-

`m!-^kC_1(m-1)!+^kC_2(m-2)!-^kC_3(m-3)!+........`

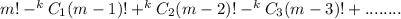
Given digits : 0,1,2,3,4,5,6,7,8,9

Prime numbers = 2,3,5,7

Now by Partial derangement the number of ways to arrange 10 numbers such that none of 4 prime numbers is in its original position will be :_

`10!-^4C_1(9)!+^4C_2(8)!-^4C_3(7)!+^4C_4(6)!\\\\=3628800-(4)(362880)+(4!)/(2!2!)(40320)-(4)(5040)+(1)(720)\\\\=3628800-1451520+241920-20160+720\\\\=2399760`

Hence, the number of ways can the digits 0,1,2,3,4,5,6,7,8,9 be arranged so that no prime number is in its original position = 2399760