Answer:

Explanation:
A function satisfying the equation
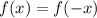 is said to be an even function. This denomination comes from the fact that the same relation is satisfied for functions of the form
is said to be an even function. This denomination comes from the fact that the same relation is satisfied for functions of the form
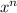 with
with
 even. Observe that if
even. Observe that if
 is twice differentiable we can derivate using the chaing rule as follows:
is twice differentiable we can derivate using the chaing rule as follows:
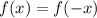 implies
implies
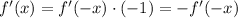
Applying the chain rule again we have:
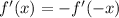 implies
implies
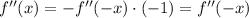
So we have that function
 is also an even function.
is also an even function.