Question

Assume that the sales of a certain appliance dealer can be approximaed y sraig were $6000 in 1982 and $ 64,000 in 1987. Let x - O represent 1982 Find the equation giving yearly alesSand then use it to predict the yearly sales in 1990.

Answer 1

`y=11,600x+6,000`

Yearly sales in 1990: $98,800.

Explanation:

We have been given that the sales of a certain appliance dealer can be approximated by a straight line. Sales were $6000 in 1982 and $ 64,000 in 1987.

If at 1982,
`x=0` then at 1987 x will be 5.

Now, we have two points (0,6000) and (5,64000).

`\text{Slope}=(64,000-6,000)/(5-0)`

`\text{Slope}=(58,000)/(5)`

`\text{Slope}=11,600`

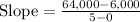
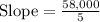
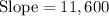
Now, we will represent this information in slope-intercept form of equation.

`y=mx+b`, where,

m = Slope,

b = Initial value or y-intercept.

We have been given that at
`x=0`, the value of y is 6,000, so it will be y-intercept.

Substitute values:

`y=11,600x+6,000`

Therefore, the equation
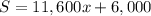`S=11,600x+6,000` represents yearly sales.

Now, we will find difference between 1990 and 1982.

`1990-1982=8`

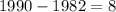
To find yearly sales in 1990, we will substitute
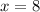`x=8` in the equation.

`S=11,600(8)+6,000`

`S=92,800+6,000`

`S=98,800`

Therefore, the yearly sales in 1990 would be $98,800.