Answer:
Marginal revenue = R'(Q) = -0.6 Q + 221
Average revenue = -0.3 Q + 221
Explanation:
As per the question,
Functions associated with the demand function P= -0.3 Q + 221, where Q is the demand.
Now,
As we know that the,
Marginal revenue is the derivative of the revenue function, R(x), which is equals the number of items sold,
Therefore,
R(Q) = Q × ( -0.3Q + 221) = -0.3 Q² + 221 Q
∴ Marginal revenue = R'(Q) = -0.6 Q + 221
Now,
Average revenue (AR) is defined as the ratio of the total revenue by the number of units sold that is revenue per unit of output sold.
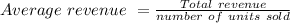
Where Total Revenue (TR) equals quantity of output multiplied by price per unit.
TR = Price (P) × Total output (Q) = (-0.3Q + 221) × Q = -0.3 Q² + 221 Q
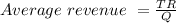
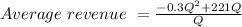
∴ Average revenue = -0.3Q + 221