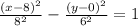Question

Write an equation of an hyperbola whose vertices are

(0,0)and(16,0), and whose foci are (18,0) and (-2,0).

Answer 1

`((x-8)^2)/(8^2)-((y-0)^2)/(6^2)=1`

Explanation:

∵ The equation of a hyperbola along x-axis is,

`((x-h)^2)/(a^2)-((y-k)^2)/(b^2)=1`

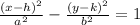
Where,

(h, k) is the center,

a = distance of vertex from the center,

b² = c² - a² ( c = distance of focus from the center ),

Here,

vertices are (0,0) and (16,0), ( i.e. hyperbola is along the x-axis )

So, the center of the hyperbola = midpoint of the vertices (0,0) and (16,0)

`=((0+16)/(2), (0+0)/(2))`

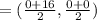
= (8,0)

Thus, the distance of the vertex from the center, a = 8 unit

Now, foci are (18,0) and (-2,0).

Also, the distance of the focus from the center, c = 18 - 8 = 10 units,

`\implies b^2=10^2-8^2=100-64=36\implies b = 6`

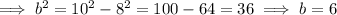
( Note : b ≠ -6 because distance can not be negative )

Hence, the equation of the required hyperbola would be,

`((x-8)^2)/(8^2)-((y-0)^2)/(6^2)=1`