Question

In a certain year, the U.S. Senate was made up of 53 Democrats, 45 Republicans, and 2 Independents who caucus with the Democrats. In a survey of the U.S. Senate conducted at that time, every senator was asked whether he or she owned at least one gun. Of the Democrats, 19 declared themselves gun owners; of the Republicans, 21 of them declared themselves gun owners; none of the Independents owned guns. If a senator participating in that survey was picked at random and turned out to be a gun owner, what was the probability that he or she was a Democrat? (Round your answer to four decimal places.)

Answer 1

There is a 47.50% probability that the chosen senator is a Democrat.

Explanation:

This can be formulated as the following problem:

What is the probability of B happening, knowing that A has happened.

It can be calculated by the following formula:

`P = (P(B).P(A/B))/(P(A))`

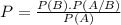
Where P(B) is the probability of B happening, P(A/B) is the probability of A happening knowing that B happened and P(A) is the probability of A happening.

In your problem we have that:

A(what happened) is the probability of a gun owner being chosen:

There are 100 people in the survay(53 Democrats, 45 Republicans ans 2 Independents), and 40 of them have guns(19 Democrats, 21 Republicans). So, the probability of a gun owner being chosen is:

`P(A) = (40)/(100) = 0.4`

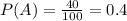
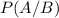`P(A/B)` is the probability of a senator owning a gun, given that he is a Democrat. 19 of 53 Democrats own guns, so the probability of a democrat owning a gun is:

`P(A/B) = (19)/(53) = 0.3585`

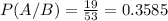
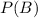`P(B)` is the probability that the chosen senators is a Democrat. There are 100 total senators, 53 of which are Democrats, so:

`P(B) = (53)/(100) = 0.53`

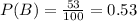
If a senator participating in that survey was picked at random and turned out to be a gun owner, what was the probability that he or she was a Democrat?

`P = (P(B).P(A/B))/(P(A)) = ((0.53)*(0.3585))/((0.40)) = 0.4750`

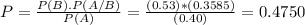
There is a 47.50% probability that the chosen senator is a Democrat.