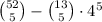Question

Counting 5-card hands from a deck of standard playing cards. A 5-card hand is drawn from a deck of standard playing cards. How many 5-card hands have at least one club? (b) Hown -card hands have at least two cards with the same rank?

Answer 1

b

Explanation:

Answer 2

5-card hands with at least one club:
`{52 \choose 5}-{39 ]choose 5}`

5-card hands with at least two cards of the same rank:
`{52 \choose 5}-{13 \choose 5}4^5`

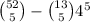
Explanation:

To determine how many 5-card hands have at least one club, we can count how many do NOT have at least one club, and then subtract that from the total amount of 5-card hands that there are.

A 5-card hand that doesn't have at least one club, is one whose 5 cards are from spades,hearts or diamonds. Since a standard deck of cards has 13 clubs, 39 of the cards are spades, hearts of diamonds. Getting a 5-card hand out of those cards, is choosing 5 cards out of those 39 cards. So there are
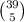`{39 \choose 5}` 5-card hands without any clubs.

The total amount of 5-card hands is
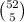`{52 \choose 5}`, since a 5-card hand is simply a group of 5 cards out of the full deck, which has 52 cards.

Therefore the number of 5-card hands that have at least one club is
`{52 \choose 5}-{39 \choose 5}`.

To determine how many 5-card hands have at least two cards with the same rank we can follow the same approach. We determine how many 5-card hands have NO cards with the same rank, and the subtract that out of the total amount of 5-card hands.

A 5-card hand that doesn't have cards of the same rank, is a group of 5 cards all from different ranks. Such hand can be made then by choosing first which 5 different ranks are going to be present in the hand, out of the 13 available ranks. So there are
`{13 \choose 5}` possible combinations of ranks. Then, choosing which card from each of the chosen ranks is the one that is going to be in the hand, is choosing which of 4 cards from EACH rank is going to be in the hand. So for each rank there are 4 availble choices, and so there are
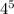`4^5` possible ways to choose the specific cards from each rank that will be in the hand. So the amount of 5-card hands with all ranks different is
`{13 \choose 5}\cdot{4^5}`

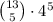
Therefore the amount of 5-card hands with at least two cards with the same rank is
`{52 \choose 5}-{13 \choose 5}\cdot4^5`